現代物理對基督徒奧祕觀的啟發(上)——量子力學（Quantum Mechanics） 是20世紀物理學最偉大的革命之一，它描述的是「微觀世界」（原子、電子、光子、分子等極小尺度）的物理行為，與我們日常經驗的「經典物理」（牛頓力學、電磁學）完全不同

量子力學（Quantum Mechanics） 是20世紀物理學最偉大的革命之一，它描述的是「微觀世界」（原子、電子、光子、分子等極小尺度）的物理行為，與我們日常經驗的「經典物理」（牛頓力學、電磁學）完全不同。

量子力學是描述粒子：

• 同時具有「波動性」與「粒子性」
• 狀態可以「疊加」
• 測量會「瞬間塌縮」
• 兩個粒子可以「量子糾纏」的物理理論

。

量子力學的幾個最核心、也最違反直覺的概念（通俗解釋）：

1. 波粒二象性
   電子、光子這些粒子，既像粒子（有明確位置），又像波（會發生干涉、繞射）。
   → 著名的「雙縫實驗」：電子一個一個打出去，卻能在螢幕上形成干涉條紋，像波一樣。
2. 量子疊加（Superposition）
   在沒被觀測之前，一個量子系統可以同時處於多種狀態的「疊加」。
   → 最有名的比喻：薛丁格的貓——在打開盒子前，貓同時處於「又活又死」的疊加態。
3. 測量塌縮（Wave function collapse）
   一旦你去「觀測」或「測量」，疊加態會瞬間塌縮成單一確定狀態。
   → 這就是為什麼你永遠看不到「半死半活的貓」，一觀測就變成明確的活或死。
4. 量子糾纏（Entanglement）
   兩個粒子一旦糾纏，它們的狀態會瞬間關聯，即使相隔光年之遠，測量其中一個，另一個會瞬間改變。
   → 愛因斯坦稱之為「鬼魅般的超距作用」（spooky action at a distance）。
5. 不確定性原理（海森堡不確定性原理）
   你不可能同時精確知道一個粒子的「位置」和「動量」（速度×質量）。知道越準確，另一個就越模糊。
   → 微觀世界沒有「絕對精確的軌道」這種東西。
6. 能量量子化
   能量不是連續的，而是像樓梯一樣一階一階的（量子）。
   → 這解釋了為什麼原子光譜是分立的線，而不是連續的彩虹。

量子力學的數學基礎（簡單說）

• 粒子的狀態用「波函數」ψ 描述
• |ψ|² 表示在某位置找到粒子的機率密度
• 核心方程：薛丁格方程（Schrödinger Equation）
  iℏ ∂ψ/∂t = Ĥψ （描述波函數如何隨時間演化）

為什麼量子力學這麼重要？

• 所有現代科技的基石：半導體、晶片、雷射、MRI、GPS、量子電腦…全部靠量子力學
• 解釋了化學鍵、物質結構、太陽為什麼能發光
• 正在引發第二次量子革命（量子計算、量子通訊、量子感測）

一句最白話的總結：

「在原子世界裡，東西不是『確定在那裡』，而是『有機率在那裡』；你不去看它時，它可以同時在好幾個地方、好幾種狀態；你一看，它才『決定』要變成哪一種。」這就是量子力學最顛覆之處——它告訴我們：宇宙在最深層的本質，是機率、疊加與糾纏，而非我們直覺中的「確定性」。

原子軌域（atomic orbital）完全屬於量子力學的核心概念，而且是量子力學最經典、最重要的應用之一。

為什麼原子軌域「只能用量子力學」來解釋？

經典物理（波耳模型以前）	量子力學（軌域模型）
假設電子像行星一樣在固定軌道繞原子核跑	電子根本沒有固定軌道！
電子應該會持續輻射電磁波，能量越來越少，最後掉到原子核	完全違反實驗！原子是穩定的
無法解釋化學鍵、光譜為什麼是一條一條的線	完美解釋

原子軌域到底是什麼？（白話版）

原子軌域不是「電子跑的小路」，而是：「電子在原子周圍出現的機率雲」或者說：「電子在空間某個區域被找到的機率密度分佈」

• 1s 軌域 → 球形雲，越靠近原子核機率越高
• 2p 軌域 → 啞鈴形，有兩個葉片
• 3d 軌域 → 更複雜的花瓣或四葉形
  這些形狀全部來自薛丁格方程的解！

關鍵的量子力學來源（四個量子數）

每個原子軌域都由四個量子數完全決定，這四個數字全部來自量子力學：

1. 主量子數 n（1, 2, 3…）→ 決定能量與大小
2. 角量子數 ℓ（0 到 n-1）→ 決定形狀（s, p, d, f）
3. 磁量子數 mℓ → 決定空間方向
4. 自旋量子數 ms（+1/2 或 -1/2）→ 電子自旋

沒有量子力學，這四個量子數根本不存在，也就沒有軌域的概念。

歷史小結

• 1913年：波耳模型（還是有軌「道」）→ 半經典
• 1926年：薛丁格發表波動力學 + 海森堡矩陣力學 → 真正量子力學
• 1926-1927年：誕生了「軌域（orbital）」這個詞（取代了舊的「軌道 orbit」）
• 1930年代：軌域圖像變成現代化學的基礎（保羅原理、洪德規則、构造原理）

結論：
原子軌域不是「有點量子」，而是「100% 量子力學的產物」。如果沒有量子力學，就不會有 s、p、d、f 軌域，也不會有現代化學鍵理論、週期表解釋、半導體、雷射……幾乎所有現代科技都會崩塌。

所以當你看到課本畫的那些球形、啞鈴形、四葉草形狀時，請記得：那不是電子在跑的路，而是「量子機率雲」的視覺化——這就是量子力學最美的畫作之一。

原子軌域、分子軌域和混成軌域是描述分子中電子分佈的三個相關概念

• 原子軌域： 指的是單一原子中電子出現的機率區域，例如 ss𝑠、 pp𝑝、 dd𝑑軌域。
• 混成軌域： 指的是在形成化學鍵前，同一原子中能量相近的軌域（如 ss𝑠軌域和 pp𝑝軌域）重新組合而成的等價新軌域。它用於解釋分子結構，例如甲烷的 sp3s p cubed𝑠𝑝3混成軌域形成正四面體結構。
• 分子軌域： 指的是在分子中，電子同時在多個原子核之間運動的區域。它是原子軌域組合而成，通常使用「原子軌域線性組合」（LCAO-MO）方法來描述。 

總結來說，原子軌域是原子的基本組成部分，分子軌域描述了整個分子的電子行為，而混成軌域則是原子軌域在分子鍵結過程中重組後形成的新軌域，用來解釋分子結構和鍵結特性。

原子軌域

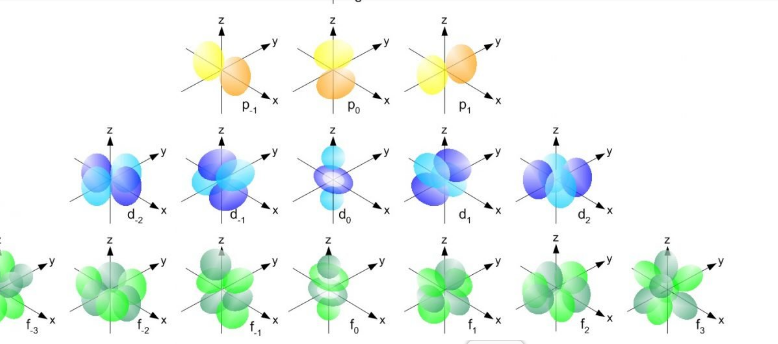
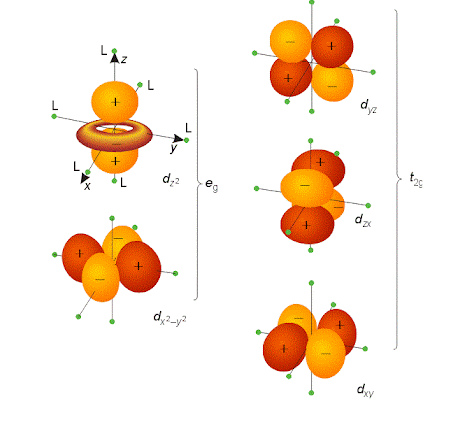
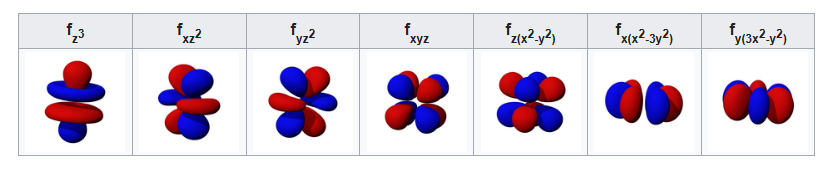
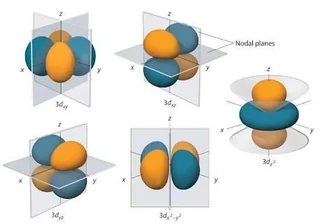
分子軌域